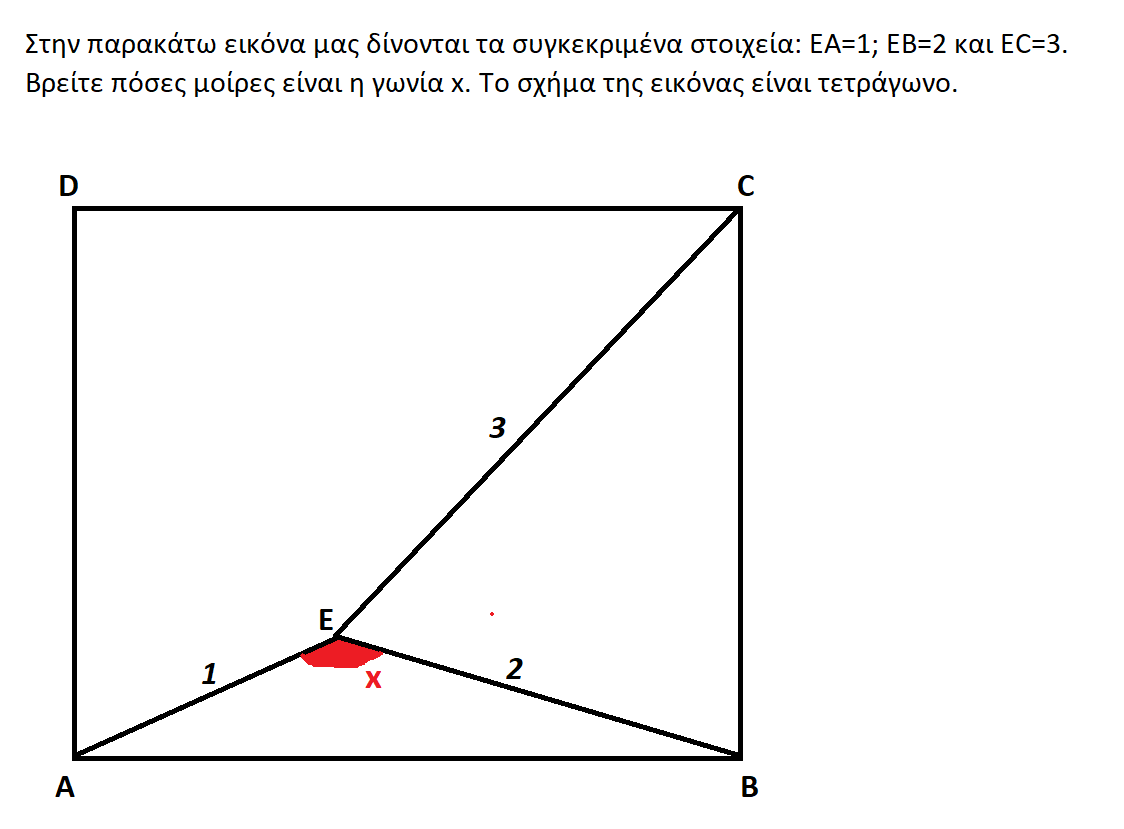
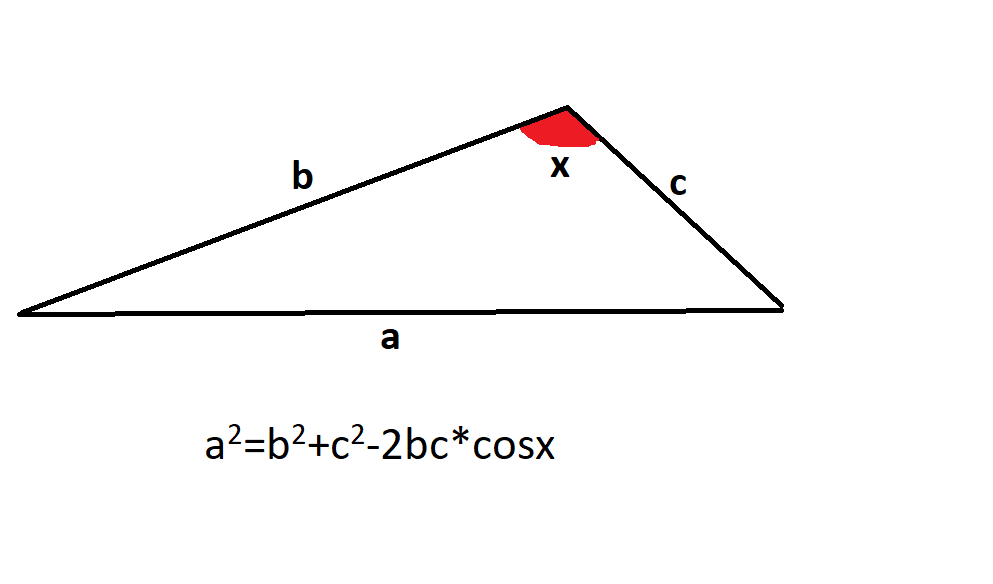Στην παρακάτω εικόνα μας δίνονται τα συγκεκριμένα στοιχεία: EA=1; EB=2 και EC=3. Βρείτε πόσες μοίρες είναι η γωνία x. Το σχήμα της εικόνας είναι τετράγωνο. Το πρόβλημα θέλει χαρτί και μολύβι.
το μονο που με βοηθανε οι αναμνησεις απο το σχολειο ειναι να βρω το μηκος ΑΒ και αφου ειναι τετραγωνο ολες τις πλευρες. γυμνασιου η λυκειου ειναι η ασκηση. κατι μου λεει οτι πρεπει να τραβηξουμε την προεκταση της ΒΕ να τεμνει την ΑD .
1 «Μου αρέσει»
Αρκεί να βρούμε το μήκος της πλευράς του τετραγώνου. Μετά είναι νόμος συνημιτονων.
1 «Μου αρέσει»
αφου στα 2 τριγωνα ξερουμε τις 2 πλευρες δεν μπορουμε να βρουμε την τριτη; το τετραγωνο της υποτεινουσας ισουτε με το αθροισμα των τετραγωνων των αλλων 2 πλευρων
1 «Μου αρέσει»
Στα ορθογώνια τρίγωνα.
2 «Μου αρέσει»
πω πω πρεπει να ξαναδιαβασω γεωμετρια
2 «Μου αρέσει»
Μια καθόλου κομψή λύση, αλλά τι τους θέλουμε τους υπολογιστές
Πιστεύω μια κομψή λύση μπορεί να βρεθεί αν χρησιμοποιήσεις συμμετρία και καθρεπτίσεις το σχήμα οριζόντια και κάθετα σχηματίζοντας ένα τετράγωνο με μήκος 2L, αλλά αρκετά η κατάδυση στα μαθηματικά του Λυκείου 
1 «Μου αρέσει»
Χωρίς να πας σε Wolfram σπας τον παρονομαστή σε {l}^2 και επιλύεις δευτεροβάθμια με άγνωστο το {l}^2 και κρατάς προφανώς μόνο τη θετική ρίζα γιατί αρνητικό μήκος δεν υπάρχει.
Άρα η τελική εξίσωση θα έχει τη μορφή
\frac{(l^2+3)^2}{16l^2} + \frac{(l^2-5)^2}{16l^2} = 1
βρίσκοντας το {l} πας με νόμο συνημιτόνων και βρίσκεις γωνία Χ
Θα βρεις όμως 2 τιμές για το l και θα πρέπει με κάποιον τρόπο να απορριφθεί η 1
1 «Μου αρέσει»
Προτιμώ λίγη ωμή διανυσματική βία παρά να προσπαθήσω να θυμηθώ οποιονδήποτε νόμο.
έχουμε (δεν βάζω βελάκια)
- AE^2 = 1
- BE^2 = 4
- CE^2 = 9
ΒΕ = ΒΑ + ΑΕ
CΕ = CB + ΒΑ + ΑΕ
AE = xi + yj
AB = li
BC = lj
AB AE = lx
BC AE = ly
από 1:
- x^2+y^2=1
από 2:
l^2 + 1 + 2BAAE =4
- 2lx = l^2 - 3
από 3:
l^2 + l^2 + 1 + 2CBAE + 2BAAE = 9
- 2lx + 2ly = 2l^2 - 8
από 5. και 6. :
- 2ly = l^2 - 5
Οπότε αντικαθιστούμε τα x,y από 5,7 στην 4 και λύνουμε.
1 «Μου αρέσει»
Το οποίο σε καταλήγει στις εξισώσει που έγραψα
1 «Μου αρέσει»
μοιάζουν αλλά έχουμε κάποιες διαφορές. πχ έχεις l^2 +3 ενώ εγώ έχω l^2 -3.
1 «Μου αρέσει»
Χαχαχα… Σε σωστό δρόμο προς την λύση του προβλήματος είσαι περίπου @Asfodelus αλλά για να βρεθεί λύση πρέπει να εφαρμοστεί και η θεωρία του Πυθαγόρα. Επίσης πρέπει να γίνουν και κάποιες τροποποιήσεις στην εικόνα που είχα δώσει πιο πάνω. 
Στην παρακάτω εικόνα δίνω μια μικρή βοήθεια. Επίσης για να βρεθεί το αποτέλεσμα πρέπει να γίνει μια τροποποίηση στην εικόνα στην εικόνα που είχα δώσει παραπάνω στο πρόβλημα. Και μια άλλη βοήθεια που δίνω είναι ότι πρέπει να εφαρμοστεί η θεωρία του Πυθαγόρα.
Χαχαχα… Δώσε αποτέλεσμα
Σε σωστό δρόμο είσαι περίπου
@anon8758935 αυτό που γράφεις είναι ο νόμος των συνημιτόνων. Στην περίπτωση του πυθαγορείου το συνημίτονο των 90ο είναι μηδέν.
2 «Μου αρέσει»
Η απάντηση μου χρησιμοποιεί το γενικευμένο πυθαγόρειο θεώρημα στις δυο διαστάσεις, γνωστό και σαν νόμο των συνημίτονων. Δηλαδή τον τύπο που έδωσες.Είναι μια λύση που δεν έχει κανένα ιδιαίτερο μαθηματικό ενδιαφέρον για να ασχοληθείς περισσότερο 
Ενδιαφέρον θα ήταν αν υπήρχε μια έξυπνη λύση (πχ να κάνεις κάποιες περιστροφές ή καθρεπτισμούς και να εκμεταλλευτείς μια γεωμετρία).
Μια μορφοποίηση του προβλήματος σαν ένα πρόβλημα περιορισμών και να το περάσεις σε κάποιον geometry containt solver (όπως πχ τον ledas) έχει κάποιο υπολογιστικό ενδιαφέρον… Αυτή η απόσταση είναι τόσο, αυτό είναι κάθετο σε αυτό, βρες μου μια λύση.
1 «Μου αρέσει»
Είπα να το φτάσω μέχρι το τέλος. Δεν βλέπω να κάνω κάπου λάθος.
Με q=l^2 έχουμε την εξίσωση:
q^2 - 10q +36=0
οπότε ανοίγω για τις πράξεις:
> ipython --pylab
Python 3.8.2 (default, Feb 26 2020, 22:21:03)
Type 'copyright', 'credits' or 'license' for more information
IPython 7.13.0 -- An enhanced Interactive Python. Type '?' for help.
Using matplotlib backend: Qt5Agg
In [1]: a=1;b=-10;c=18;
In [2]: d=b**2-4*a*c
In [3]: q = array([(-b + sqrt(d))/2/a, (-b - sqrt(d))/2/a])
In [4]: arccos((5-q)/4)
Out[4]: array([2.29353057, 0.84806208])
In [5]: _*180/pi
Out[5]: array([131.40962211, 48.59037789])
οι 131 μοίρες απορρίπτονται. Ίσως και όχι δεν υπαγορεύει η εκφώνηση ότι το Ε είναι μέσα στο τετράγωνο.
@lucinos στο περίπου κοντά είσαι προς την λύση απλά θέλω να μου δώσεις μια σταθερή τιμή για το πόσες μοίρες είναι η γωνία x. Είναι 131 ή δεν είναι; Και αν δεν είναι πόσο είναι;
άκυρο, σε ποιο τεταρτημόριο πέφτει το Ε είναι από τις συντεταγμένες x,y.
αφού 2lx=(q-3), 2ly=q-5
In [6]: q-3,q-5
Out[6]: (array([ 4.64575131, -0.64575131]), array([ 2.64575131, -2.64575131]))
Η 131 μοίρες είναι η έγκυρη εντός τετραγώνου.
Προφανώς ότι με τις τιμές των l και της γωνίας υπολογίζεις τα υπόλοιπα και βλέπεις αν ισχύουν το σύνολο των 180 μοιρών για όλα τα τρίγωνα