Γράψτε ένα πρόγραμμα που να υπολογίζει το άθροισμα των αριθμών που διαιρούνται με το 3 και με το 5 μέχρι ένα δεδομένο αριθμό. Οποιαδήποτε γλώσσα
Για να δούμε αν υπάρξει ενδιαφέρον 
Γράψτε ένα πρόγραμμα που να υπολογίζει το άθροισμα των αριθμών που διαιρούνται με το 3 και με το 5 μέχρι ένα δεδομένο αριθμό. Οποιαδήποτε γλώσσα
Για να δούμε αν υπάρξει ενδιαφέρον 
μήπως ήθελες να γράψεις ή και όχι και;
Γιατί τώρα εννοείς απλώς τα πολλαπλάσια τού 15.
Αλλά οκ (python)
def souma(n):
i = 15
s = 0
while True:
if i > n: return s
s += i
i += 15
Αν είναι ή τελικά η πρόταση, θα είναι κάπως έτσι :
#!/usr/bin/env python
arithmos=int(input("Enter a number: "))
x=0
summ=0
if arithmos<3:
print(summ)
elif (arithmos>=3)and(arithmos<5):
summ=3
print(summ)
elif arithmos==5:
summ=8
print(summ)
else:
summ=8
for x in range(6,arithmos+1):
if (x%3==0)or(x%5==0):
summ+=x
print(summ)
καλό είναι να συνηθίζουμε τον κόσμο με συναρτήσεις
def souma(n):
s = 0
i = 3
while True:
if i > n: return s
if i%3 == 0 or i%5 == 0: s += i
i += 1
Θεωρώ να διαιρούνται με 3 ή 5, μέχρι και το δεδομένο αριθμό, σε C:
#include <stdio.h>
int sum_calculate(int user_value) {
int i, sum = 0;
for(i = 0; i <= user_value; i++) {
if((i % 3 == 0) || (i % 5 == 0)) {
sum = sum + i;
}
}
return(sum);
}
int main(int argc, char *argv[]) {
int user_value;
printf("Enter a value:");
scanf("%d", &user_value);
printf("SUM: %d\n", sum_calculate(user_value));
return 0;
} επειδή έχεις συνάρτηση για τον υπολογισμό
επειδή έχεις συνάρτηση για τον υπολογισμό 
Ας δώσω και το «ολοκληρωμένο» πρόγραμμα σε python
#!/bin/python3
#proklisi1.py
def souma(n):
s = 0
i = 3
while True:
if i > n: return s
if i%3==0 or i%5==0: s += i
i += 1
def main(n=None):
if n is None:
n = int(input('Δώσε αριθμό: '))
print ("Άθροισμα:", souma(n))
if __name__ == '__main__':
import sys
try:
n = int(sys.argv[1])
main(n)
except IndexError:
main()
except ValueError:
print(':P')
Να ευχαριστήσω κατ’ αρχήν τις πρώτες συμμετοχές. Ελπίζω να το βρήκατε ένα ευχάριστο πρόβλημα και να μάθαμε και όσοι πήραν μέρος με κώδικα και όσοι το διαβάζουν κάτι παραπάνω. Σκοπός είναι να ξεσκουριάζουμε, να βλέπουμε κώδικα σε άλλες γλώσσες, και να κάνουμε χαβαλέ, και όχι να κάνουμε κάποιο διαγωνισμό.
Με βάση αυτά μερικές παρατηρήσεις. Σε όσους επέλεξαν την C/C++ γιατί διαλέξατε ως τύπο τον int; Ένας unsigned long long δεν θα ταίριαζε εδώ καλύτερα; (τουλάχιστον σε μια ποιο γενική περίπτωση). Επίσης αν ήθελα να πω ή δεν θα έλεγα και. Το πρόβλημα είναι σαφές. Λέει και, καθώς για δυο συγκεκριμένους αριθμούς που δεν επιλέχθηκαν τυχαία. Αλλιώς για δυο τυχαίους φυσικούς αριθμούς θα ήταν μάλλον μπερδεψοδουλειά  Λύσατε λοιπόν το λάθος πρόβλημα
Λύσατε λοιπόν το λάθος πρόβλημα 
Εκτιμώ βέβαια το γεγονός πως πήγατε να λύσετε το δύσκολο πρόβλημα, μιας και το ή μοιάζει δυσκολότερο, αλλά θα διαφωνήσω σε αυτό. Έθεσα το δύσκολο πρόβλημα, όχι το εύκολο. Αν λύσεις το δύσκολο πρόβλημα του και, τότε το πρόβλημα του ή είναι μάλλον προφανές 
Ξέρουμε βέβαια όλοι μας πως αν τραβήξω την διαγώνια σε ένα παραλληλόγραμμο το τρίγωνο που θα προκύψει θα έχει το μισό εμβαδόν, αλλά το λέω για να μην λέτε πως δεν σας μπέρδ βοήθησα 
Περιμένω τις βελτιωμένες λύσεις σας 
Μα αν φτιάξουμε κλειστό τύπο, τότε γιατί να χρησιμοποιήσουμε υπολογιστή; ![]()
Για τον ίδιο λόγο που η δεσμευμένη λέξη constexpr υπάρχει στην C++ 
Σε ένα βιβλίο προγραμματισμού, πάντως δίνει μια λύση σε αλγοριθμικό \mathbf{O}(n) πάνω κάτω σαν αυτή που δώσατε.
Κρίμα γιατί το πρόβλημα είναι πολύ βαθύ. Αν έχεις μια συνάρτηση \sum(x_1,max) μπορείς να υπολογίσεις με αυτή το \sum(x_1\,\text{or}\, x_2, max ); Και πιάνουμε ήδη πολύ επικίνδυνα μονοπάτια 
Έχω συνηθίσει να χρησιμοποιώ τους απλούς τύπους πρώτα και να τους αλλάζω μόνο αν προκαλούν πρόβλημα και επειδή δεν διευκρινίζεται μέγιστη τιμή του δεδομένου αριθμού δεν το έδωσα σημασία. Αλλά όντως το unsigned long long ταιριάζει καλύτερα.
Περιμένω να δω και άλλες γλώσσες, είμαι σίγουρος ότι η κοινότητα καλύπτει μεγάλο εύρος. ![]()
Επειδή το βρήκα  , δεν θα το ποστάρω ακόμα, αλλά θα δώσω λίγο χρόνο και στους υπόλοιπους, όσο διαμορφώνω ένα πλήρως λειτουργικό πρόγραμμα τερματικού που θα κάνει αυτή τη δουλιά για σετ διαρετών που θα δίνεται από τον χρήστη, και θα έχει και μενού βοήθειας. Το παρών θα το κάνω φυσικά και ως ένα αποτέλεσμα της συνολικής εμπειρίας και όλων των προηγουμένων απαντήσεων.
, δεν θα το ποστάρω ακόμα, αλλά θα δώσω λίγο χρόνο και στους υπόλοιπους, όσο διαμορφώνω ένα πλήρως λειτουργικό πρόγραμμα τερματικού που θα κάνει αυτή τη δουλιά για σετ διαρετών που θα δίνεται από τον χρήστη, και θα έχει και μενού βοήθειας. Το παρών θα το κάνω φυσικά και ως ένα αποτέλεσμα της συνολικής εμπειρίας και όλων των προηγουμένων απαντήσεων.
Εγώ πάλι λέω να το σποϊλάρω…
Ας πάρουμε κάτι λίγο πιο γενικό από το 3 και 5, που είναι πρώτοι, οπότε ουσιαστικά το πρόβλημα ανάγεται στο ‘διαιρείται με το 15’…
Semi-efficient:
Οι παραπάνω λύσεις, με τη διαφορά ότι μπορείς αρχικά να κανεις increment κατά 15, ξεκινώντας από το ΕΚΠ των 2 αριθμών (δηλαδή 15), καθώς οτιδήποτε ενός του (Ν,Ν+15) συνόλου, όπου Ν ένας διαιρούμενος με το 15 αριμός, προφανώς δεν είναι διαιρέτης του. Still, Ο(n) complexity.
Efficient:
Ουσιαστικά αυτό που είπε ο Τάλος γεωμετρικά, γραμμένο αλγεβρικά. Με δεδομένα “a”, “b” τους δύο ακεραίους και με δεδομένο μέγιστο το “Μ”
Συνολικό time complexity: Ο(logn) -> Oυσιαστικά ή εύρεση του ΕΚΠ…
ΥΓ: Το γράψιμο σε real code το αφήνω σε εσάς, κυρίως λόγω βαρεμάρας…
Cheers
Θα δώσω και εγώ μια δική μου λύση που δεν δουλεύει πάντα, αλλά είναι καθαρό \mathcal{O}(1). Υπάρχει πλέον όλη η πληροφορία για όποιον θέλει να ενώσει τα κομμάτια, ή τουλάχιστον έτσι ελπίζω λολ
#include <cassert>
using Nat = unsigned long long;
int main() {
constexpr auto fSum = [](auto div1, auto div2, auto max) {
constexpr auto pSum = [](auto div, auto max) {
auto m = max / div;
return m * (m + 1) / 2 * div;
};
return pSum(div1, max) + pSum(div2, max) - pSum(div1 * div2, max);
};
assert(fSum(3, 5, 100) == naive_sum(3, 5, 100));
// assert(fSum(3*5, 5, 100) == naive_sum(3*5, 5, 100));
return EXIT_SUCCESS;
}
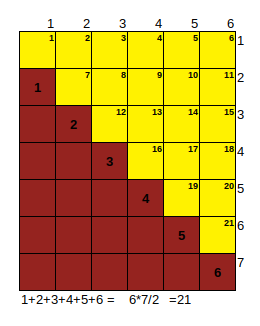
Αν έχουμε 3 διαιρέτες;
Και το συνολικό προγραμματάκι που σας οφείλω από πριν. Υλοποίηση στην αγαπημένη C++. (Ένα χρόνο είχα να την πιάσω στα χέρια μου την κούκλα με την σχολή που έμπλεξα και τα πάντα είναι java)
Για τον πλήρη κώδικα σε ανθρώπινη μορφή και το εκτελέσιμο καθώς και την εικόνα, μπορείτε να τα βρείτε στο Google drive μου. https://drive.google.com/open?id=1WdALYdz-BexNC7m3Q7dPH8RzJmccLHBy
//TDSC v1.0
//Date:13-08-2019
//Author:orfibous
//Special Thanks for their contribution to linux-user.gr members:
//@lucinos
//@kapgeorge
//@Maras
//@gmotux
//@Talos
//Compilation instractions:
//Open a terminal and move to the folder containing TDSC.cpp (this file)
//Use: g++ -o TDSC TDSC.cpp
//Use: ./TDSC --help To learn how to use the application
//TODO implement vectors to dynamicly get arguments and allow N number of divisors. One suggestion would be to also add a new argument to indicate the N number of divisors the user wants.
#include <iostream>
#include <cstring>
#include <chrono>
#include <math.h>
using namespace std;
int debugmode=0;
void sumCalculateInefficient(unsigned long long userValues[3]){
auto start = chrono::steady_clock::now();
unsigned long long sum = 0;
for(unsigned long long i = 0; i <= userValues[0]; ++i) {
if((i % userValues[1] == 0) && (i % userValues[2] == 0)) {
sum+= i;
}
}
cout << "Inefficient algorithm "<<"SUM: "<< sum << "\n";
auto end = chrono::steady_clock::now();
auto diff = end - start;
cout << chrono::duration <double, nano> (diff).count() << " ns" << endl;
return ;
}
void sumCalculateSemiEfficient(unsigned long long userValues[3]){
auto start = chrono::steady_clock::now();
unsigned long long sum = 0;
unsigned long long step = userValues[1] * userValues[2];
for(unsigned long long i = 0; i <= userValues[0]; i+= step) {
sum+= i;
}
cout << "Semi-Efficient algorithm "<< "SUM: "<< sum << "\n";
auto end = chrono::steady_clock::now();
auto diff = end - start;
cout << chrono::duration <double, nano> (diff).count() << " ns" << endl;
return ;
}
unsigned long long gcd(unsigned long long int a, unsigned long long int b){
if(b==0)
return a;
return gcd(b,a%b);
}
unsigned long long lcm(unsigned long long a,unsigned long long b){
if(a>b)
return (a/gcd(a,b))*b;
else
return (b/gcd(a,b))*a;
}
void sumCalculateEfficient(unsigned long long userValues[3]){
auto start = chrono::steady_clock::now();
unsigned long long sum = 0;
unsigned long long lcmValue = lcm(userValues[1],userValues[2]);
unsigned long long max_divisible = (userValues[0] % lcmValue == 0) ? userValues[0] : (userValues[0] - userValues[0] % lcmValue);
sum = ( ( ( max_divisible - lcmValue ) / lcmValue + 1 ) / 2 ) * ( lcmValue + max_divisible );
cout << "Efficient algorithm "<< "SUM: "<< sum << "\n";
auto end = chrono::steady_clock::now();
auto diff = end - start;
cout << chrono::duration <double, nano> (diff).count() << " ns" << endl;
return ;
}
void printInfo(){
cout <<"TDSC v1.0 (Two divisors Sum Calculator) was created as a fun summer excersice introduced by @Talos in linux-user.gr (12-08-2019).\nThe excersise was about making an algorithm that would calculate the sum of numbers divided by both 3 and 5 until a given number. \nTDSC solution is a result of all the previous answers to the problem.\nSpecial Thanks for their contribution to linux-user.gr members:\n@lucinos\n@kapgeorge\n@Maras\n@gmotux\nAuthor:@orfibous\n";
return ;
}
void printHelp(){
cout <<"Usage: ./TDSC [OPTION]... [maxNumber] [divisor_A] [divisor_B]\n";
cout <<"TDSC takes two numbers as divisors A,B and calculates the sum of all numbers from {0,MaxNumber} that are divided perfectly by both A and B. The application uses 3 different methos to calculate the sum and calculates the time it takes to execute each of them.\n";
cout <<"\nOptions list:\n -i, --info display information about this application\n -d, --debug display debug information to terminal\n -h, --help display this help and exit\n";
return ;
}
int inputControl(unsigned long long userValues[3], int argc, char *argv[]){
if(argc <= 1) cout <<"Error:No arguments please read Help (Use: ./TDSC --help)";
for(unsigned long long i= 1;i<argc-2;++i){
if(strcmp(argv[i],"-i") ==0 || strcmp(argv[i],"--info") ==0){
printInfo();
return 1;
}
if(strcmp(argv[i],"-d") ==0 || strcmp(argv[i],"--debug") ==0){
debugmode = 1;
}
if(strcmp(argv[i],"-h") ==0 || strcmp(argv[i],"--help") ==0){
printHelp();
return 1;
}
}
userValues[0] = strtoull(argv[argc-3],nullptr,0);
userValues[1] = strtoull(argv[argc-2],nullptr,0);
userValues[2] = strtoull(argv[argc-1],nullptr,0);
return 0;
}
int main(int argc, char *argv[]) {
unsigned long long userValues[3];
if (inputControl(userValues, argc, argv)) return 1;
sumCalculateInefficient(userValues);
sumCalculateSemiEfficient(userValues);
sumCalculateEfficient(userValues);
return 0;
}
Υ.Γ. Για κάποιον λόγο δεν φαίνονται τα includes στα μπλοκ κώδικα
Υ.Γ.2 Αν κάποιος θέλει όντως μπορεί να βάλει vectors και Loops στους υπολογισμούς ώστε να κάνει το πρόγραμμα να τρέχει για Ν διαιρέτες θα ήταν πολυ ενδιαφέρον.
Γενικευμενο για οποιουσδηποτε 2 αριθμους με οριο σε java:
package linuxforum;
import java.util.Scanner;
/**
* @author Petros Andrianos
*/
public class LinuxForum {
public static void calculatorSum2 ( int a, int b, int number) {
int step, calcSum;
calcSum = 0;
System.out.println("_______________________________");
System.out.println("Οι αριθμοι εναι :");
step = a * b;
for ( int i=step; i<=number; i=i+step ) {
/* Ειναι γρηγοροτερη η επιλυση του (a*b ==0) απo το (a == 0) && (b == 0) */
if ( ( i % a ) * ( i % b ) == 0 ) {
System.out.print(i + ", ");
calcSum = calcSum + i;
}
}
System.out.println("");
System.out.println("_______________________________");
System.out.println("Το αθροισμα ειναι: " + calcSum);
}
static void start() {
Scanner keyboard = new Scanner(System.in);
int a, b, sum, number;
System.out.print("Δώσε τον 1ο αριθμό: ");
a = keyboard.nextInt();
System.out.println("");
System.out.print("Δώσε τον 2ο αριθμό: ");
b = keyboard.nextInt();
System.out.println("");
System.out.print("Δώσε τον αριθμό οπου θα υπολογισω το αθροισμα\n των αριθμων που διαιρουνται με το " + a + " και το " + b + ": ");
number = keyboard.nextInt();
calculatorSum2(a, b, number);
}
public static void main(String[] args) {
start();
}
}
Κάποιος παραπονέθηκε πως περίμενε πολύ περισσότερες γλώσσες υλοποίησης. Θα τον απογοητεύσω δίνοντας μια λύση σε C++, αλλά σε μοντέρνα C++ και όχι σαν την C++ του παππού σου 
constexpr auto orSum = [](std::pair<auto, auto> divs, auto max) {
auto div1 = divs.first;
auto div2 = divs.second;
constexpr auto kSum = [](auto div, auto max) {
auto m = max / div;
return m * (m + 1) / 2 * div;
};
auto gcd = std::gcd(div1, div2);
max = max / gcd, div1 = div1 / gcd, div2 = div2 / gcd;
auto s = kSum(div1, max) + kSum(div2, max) - kSum(div1 * div2, max);
return s * gcd;
};
Δεν μοιάζει σαν μια καινούργια γλώσσα; Έκανα προσπάθεια να κάνω το πρόγραμμα γενικό. Κάτι που στην Python το έχεις χωρίς καμία απολύτως προσπάθεια. Αλλά, ΑΝ, το ζητούμενο του προγράμματος ήταν να τυπώσει απλά το orSum({3,5},100), τότε ο παραπάνω κώδικας καταρρέει σε ένα απλό print 2418 που είναι η απάντηση, και δεν θα γίνει κανένας απολύτως υπολογισμός όταν τρέχεις το πρόγραμμα. Beat me on it 
Παραθέτω μόνο την συνάρτηση υπολογισμού, χωρίς κάποια static assert και χωρίς σχόλια. Ο πλήρης κώδικάς. μαζί με κάποια σχόλια για την υλοποιηση, μπορεί να βρεθεί εδώ. Χρησιμοποιεί κάποια καινούργια χαρακτηριστικά, και ίσως έχει νόημα να προσπαθήσεις να τον γράψεις σε ποιο κλασσική γλώσσα ή σε templates για εξάσκηση. Αν υπάρχουν προβλήματα στην κατανόηση του αλγόριθμου, εδώ είμαστε  Για να γίνει compile
Για να γίνει compile
g++ -std=gnu++1z main.cppPython 
print([i for i in range(int(input("Insert number: "))) if i%3==0 and i%5==0])
και έλεγα δεν θα βρεθείς κάποιος να το σκεφτεί αυτό :)
Καλώς σας βρήκα! 