Προγραμματιστική πρόκληση Νο 10: 3*Χ +1

Προγραμματισμός
1

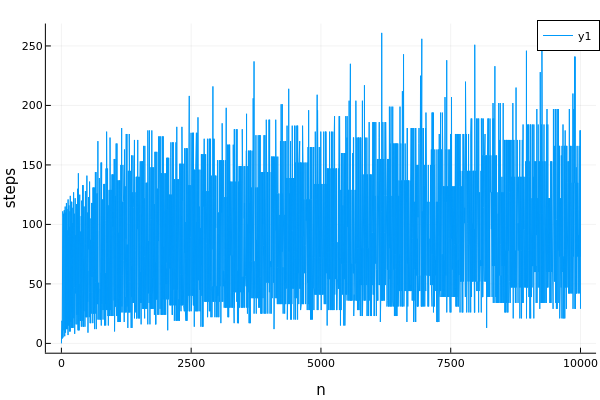
Οι κανόνες είναι απλοί: Ξεκινάμε με οποιοδήποτε θετικό ακέραιο αριθμό. Αν είναι μονός (1,3,5,..), τότε “πολλαπλασιάστε με τρία και προσθέστε ένα”, ενώ αν είναι ζυγός (2,4,6,..) και τότε “διαιρέστε με δύο”. Κάποια στιγμή η διαδικασία θα καταλήξει στον αριθμό 1. Πόσα βήματα απαιτούνται για κάποιο συγκεκριμένο αριθμό n;

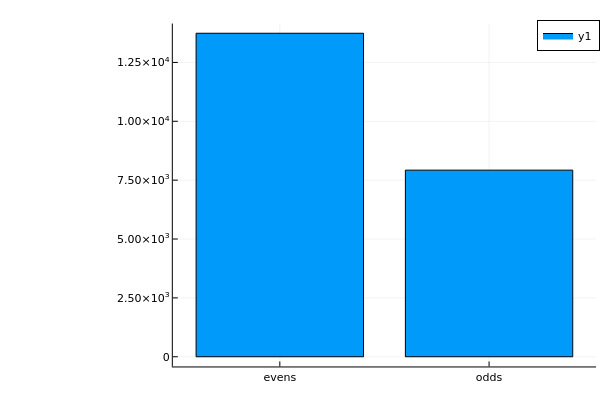
Μπορείτε να δείξετε ενδιαφέροντα αποτελέσματα σε κάποια γραφική μορφή; Πόσοι μονοί και πόσοι ζυγοί αριθμοί θα προκύψουν στην πορεία; Μέχρι κάποιο αριθμό, ας πούμε μέχρι το 10.000 ποιος αριθμός απαιτεί τα περισσότερα βήματα μέχρι να φτάσει στον αριθμό 1;

Extra πρόκληση: Μπορείτε να υπολογίσετε τον αριθμό, ελαχιστοποιώντας τις πράξεις σε κάποιες περιπτώσεις;

Ένα εύκολο πρόγραμμα αυτή την φορά, δοκιμάστε με οποιαδήποτε γλώσσα προγραμματισμού και παρουσιάστε την λύση σας εδώ. Ένα ποιο ενδιαφέρον ερώτημα βέβαια είναι γιατί συμβαίνει αυτό; Αν καταφέρετε να το αποδείξετε μην παρουσιάσετε την απόδειξη σας εδώ, αλλά σε κάποιο μαθηματικό περιοδικό. Είναι ένα από τα ποιο δύσκολα άλυτα προβλήματα των μαθηματικών, αλλά ποτέ δεν ξέρεις :slight_smile:

Hint: Collatz Conjecture

2 «Μου αρέσει»
2

Μια γρήγορη λύση σε Python

#!/usr/bin/python3
while True:
    try:
        steps=0
        number=int(input("Δώσε έναν ακέραιο : "))
        if number < 0:
            print("Θέλουμε θετικό ακέραιο")
            continue
        while number > 0:
    
            if number%2 != 0:
                print("Ο αριθμός είναι περιττός")
                number = number*3 + 1
                steps+=1
            else:
                print("Ο αριθμός είναι άρτιος")
                number = int(number/2)
                steps+=1
            print(number)
            if number == 1:
                print("H διαδικασία ολοκληρώθηκε σε",steps,"βήματα")
                break
            else:
                continue
        
    except ValueError as er:
        print(er,"Ο αριθμός που δόθηκε δεν είναι ακέραιος")

edit: και μια λύση με μέγιστο αριθμό προσπαθειών σε εύρος αριθμών

#!/usr/bin/python3

def numfunc(number):

    try:
        steps=0
        #number=int(input("Δώσε έναν ακέραιο : "))
        if number < 0:
            print("Θέλουμε θετικό ακέραιο")
        while number > 0:
    
            if number%2 != 0:
                #print("Ο αριθμός είναι περιττός")
                number = number*3 + 1
                steps+=1
            else:
                #print("Ο αριθμός είναι άρτιος")
                number = int(number/2)
                steps+=1
            # print(number)
            if number == 1:
                #print("H διαδικασία ολοκληρώθηκε σε",steps,"βήματα")
                return steps
                
                
            
    except ValueError as er:
        print(er,"Ο αριθμός που δόθηκε δεν είναι ακέραιος")
        
max_steps_dict={}
for i in range(1,10001):
    
    max_steps_dict.update({i:numfunc(i)})

max_key = max(max_steps_dict, key=lambda k: max_steps_dict[k])

print("O αριθμός",max_key,"είχε τα περισσότερα βήματα",max_steps_dict[max_key],"τον αριθμό")
1 «Μου αρέσει»
3

Μια συναρτησιακή προσέγγιση με Julia (όμοια γίνεται με Python, Ruby, …)

cache = Dict(1 => 0)
function count(n)
    if ! haskey(cache, n)
        cache[n] = 1 + count(iseven(n) ? div(n, 2) : 3*n + 1)
    end
    return cache[n]
end

Και με λίγο array programming με broadcasting

nmax = 10_000
steps = count.(1:nmax)

Πλοτάροντας τα βήματα στο εύρος

using Plots
plotly()
plot(1:nmax, steps, xlabel = "n", ylabel = "steps")

plot1
Για το σύνολο μονών/ζυγών στη πορεία

evens = length(filter(iseven, keys(cache)))
bar(["evens", "odds"], [evens, length(cache) - evens])

plot2
Ή όμοια με τα steps παραπάνω εφόσον θέλουμε απλά το πλήθος

evens = sum(iseven.(keys(cache)))

Για σύγκριση στη Ruby, μια αρκετά αντικειμενοστραφή γλώσσα

evens = cache.keys.select{ |x| x.even? }.length

και με λίγο syntactic sugar

evens = cache.keys.select(&:even?).length

Τέλος για τον αριθμό με τα περισσότερα βήματα

julia> println("(steps, n) = ", findmax(steps))
(steps, n) = (261, 6171)
3 «Μου αρέσει»